09年统计师《统计工作实务》第九章辅导讲义(3)
发布时间:2011-10-22 共1页
① 移动平均法
通过对时间数列相邻各项求平均数作为趋势值或预测值的平滑或预测方法,称为移动平均法。它具体可分为简单移动平均法和加权移动平均法。
a. 简单移动平均法
简单移动平均法是将最近的K期数据加以平均,作为移动中项的趋势测定值。
设移动时期项数为k,则第t期的移动平均值为:

注意:当k取奇数或偶数的不同形式时,处理方法有区别。对于k取奇数时,可直接运用公式(3·12)即可;当k取偶数时,要在第一次对原数列作移动平均后,对所得新数列再做一次相邻两项的移动平均,这样才能完成中心化。
例12 下表是1991-2000年我国的原煤产量数据,计算移动项数k=3,k=4时的反映趋势变动的新数列。
表3-16 我国1991-2000年原煤产量数据
| 年份 | 1991 | 1992 | 1993 | 1994 | 1995 |
| 产量(亿吨) | 10.87 | 11.16 | 11.50 | 12.40 | 13.61 |
| 年份 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 产量(亿吨) | 13.97 | 13.37 | 12.50 | 10.45 | 9.98 |
解:k=3时,移动项数为奇数,根据公式(3·21)得到
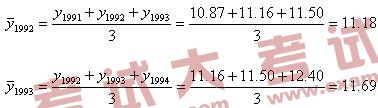
依此类推,最终结果汇集在表3-17中
当k=4时,移动项数为偶数,要移动两次,第一次移动运用公式(3·21)
得到:
依此类推可得到表中第四列k=4时的第一次移动平均。这时求出的移动平均数还不能作为趋势值,因为他们代表的时期不明确。因此要计算二次移动平均值来代表第三期的长期趋势,即进行中心化。
第二步,对k=4时的第一次移动平均的结果(第四列)进行中心化处理。

依此类推得到表3-17的第五列。
| 年份 | 产量 | 移动平均数 | ||
| K=3 | K=4 | |||
| 第一次移动平均 | 第二次移动平均 | |||
| 1991 | 10.87 | - | ||
| 1992 | 11.16 | 11.18 | 11.48 | |
| 1993 | 11.50 | 11.69 | 11.83 | |
| 1994 | 12.40 | 12.50 | 12.17 | 12.52 |
| 1995 | 13.61 | 13.33 | 12.87 | 13.15 |
| 1996 | 13.97 | 13.77 | 13.43 | 13.44 |
| 1997 | 13.73 | 13.40 | 13.45 | 13.06 |
| 1998 | 12.50 | 12.23 | 12.66 | 12.16 |
| 1999 | 10.45 | 10.98 | 11.67 | - |
| 2000 | 9.98 | - | - | |
从表3-17的计算结果看,我国的原煤产量经历了先高后低的发展态势。
a. 加权移动平均法
加权移动平均法是对各期指标值进行加权后计算移动平均数。在使用加权移动平均法时,一般计算奇数项加权移动数,各期权数以二项展开式为计算基础,使得中项时期指标值的权数最大,两边对称,越靠边的项权值越小。


